Kunci Jawaban
Kunci Jawaban Matematika Kelas 9 SMP Halaman 226 227 228, Kekongruenan dan Kesebangunan
Kunci jawaban Matematika Kelas 9 SMP Halaman 226 227 228 Kurikulum 2013, Kekongruenan dan Kesebangunan.
Editor: Tim TribunTrends
Kunci jawaban Matematika Kelas 9 SMP Halaman 226 227 228 Kurilkulum 2013, Kekongruenan dan Kesebangunan.
TRIBUNTRENDS.COM - Pelajari kunci jawaban Matematika Kelas 9 halaman 226, 227, dan 228 Kurikulum 2013, Latihan 4.2 Kekongruenan Dua Segitiga. Dalam buku Matematika kelas 9 Kurikulum 2013 (K13) untuk SMP/MTs Revisi 2018, terdapat kunci jawaban Matematika Kelas 9 SMP halaman 226, 227, dan 228 SMP/MTs Revisi 2018, Bab IV Kekongruenan dan Kesebangunan. Artikel berikut menjelaskan kunci jawaban Matematika Kelas 9 SMP halaman 226, 227, dan 228 Kurikulum 2013 Semester 2. Kunci jawaban Matematika ini dapat ditujukan kepada orang tua atau wali untuk mengoreksi hasil belajar anak.
Kunci jawaban Matematika Kelas 9 halaman 226 227 228 Kurikulum 2013 Semester 2
Latihan 4.2 Kekongruenan Dua Segitiga
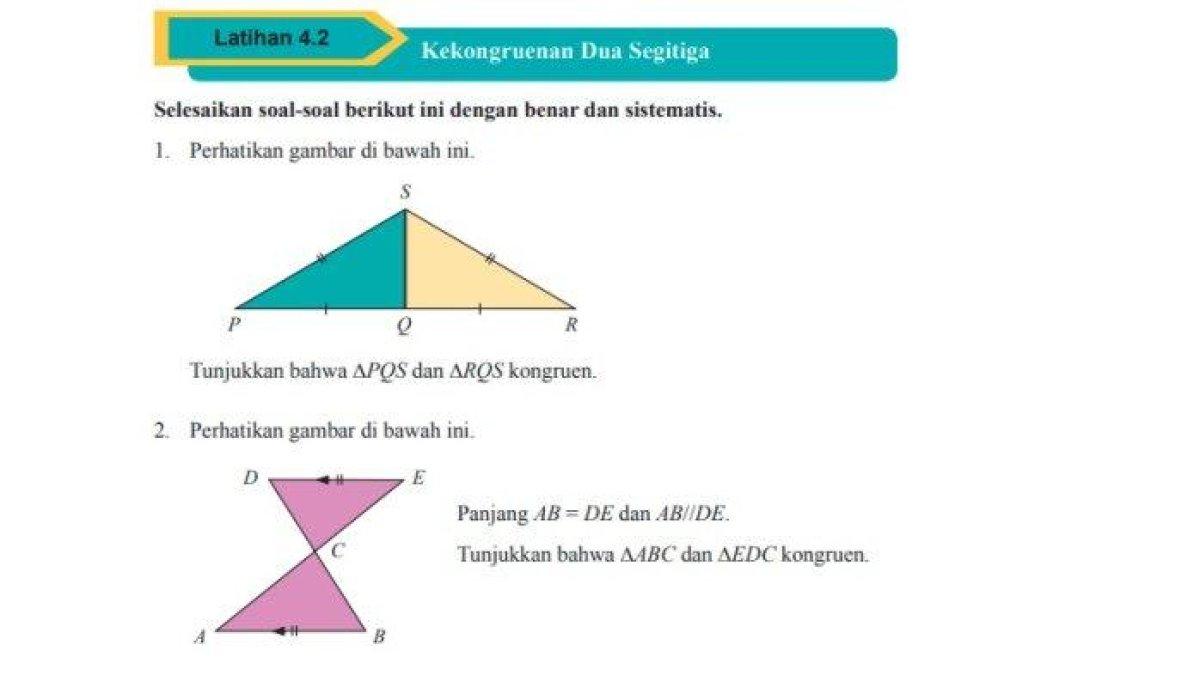
1. Tunjukkan bahwa ∆PQS dan ∆RQS kongruen.
Kunci Jawaban:
Bangun kongruen adalah dua atau lebih bangun yang memiliki bentuk dan ukuran yang sama. Bangun dikatakan kongruen apabila sama persis, baik dari bentuk maupun ukurannya.
Syarat bangun kongruen ada dua. Pertama, sisi-sisi yang bersesuaian harus sama panjang. Kedua, sudut-sudut yang bersesuaian harus sama besar.
Kedua syarat bangun kongruen tersebut saling berkesinambungan. Apabila syarat pertama terpenuhi, otomatis syarat kedua juga terpenuhi, begitu pula sebaliknya.
PQ = RQ (diketahui pada gambar)
QS (pada ΔPQS) = QS (pada ΔRQS)
PS = RS (diketahui pada gambar)
Jadi, ΔPQS dan ΔRQS kongruen berdasarkan kriteria sisi – sisi – sisi.
2. Panjang AB = DE dan AB//DE. Tunjukkan bahwa ∆ABC dan ∆EDC kongruen.
Kunci Jawaban:
AB = DE
∠ DCE = ∠ ACB (bertolak belakang)
∠ ABC = ∠ CDE (berseberangan)
Jadi, ΔABC dan ΔCDE kongruen berdasarkan kriteria sisi, sudut, sudut.
3. Titik C adalah titik pusat lingkaran. Tunjukkan bahwa dua segitiga pada gambar di samping adalah kongruen.
Kunci Jawaban:
| Jawaban Alternatif Hal Apa yang Perlu Diperhatikan dalam Penerapan Experiential Learning? PPG 2025 |

|
|---|
| Jawaban: Persiapan Apa Saja yang Dilakukan PT Penyelenggara PPG untuk Mempersiapkan UT? |

|
|---|
| Jawaban: Bagamaimana Menurut Saudara Hal-hal yang Dapat Ditingkatkan dari Pelaksanaan UT? |

|
|---|
| Jawaban PPG 2025: Setelah Anda Mempelajari Pembelajaran Sosial Emosional, Modul 2 Topik 2 |

|
|---|
| JAWABAN Bagaimana Menerapkan Experiential Learning dalam Pembelajaran Bersama dengan Guru Lain? |

|
|---|





