Kunci Jawaban
Kunci Jawaban Matematika Kelas 9 SMP Halaman 254 255: Tunjukkan Bahwa Segitiga ADB dab ABC Sebangun!
Yuk simak kunci jawaban Matematika Kelas 9 SMP halaman 254 255 Kurikulum Merdeka. Tunjukkan bahwa segitiga ADB dan ABC sebangun!
Editor: Tim TribunTrends
Yuk simak kunci jawaban Matematika Kelas 9 SMP halaman 254 255 Kurikulum Merdeka. Tunjukkan bahwa segitiga ADB dan ABC sebangun!
TRIBUNTRENDS.COM - Pelajari kunci jawaban Matematika Kelas 9 SMP pada halaman 254 dan 255. Buku Matematika Kelas 9 SMP halaman 254 dan 255 berisi soal Latihan 4.4. Soal pada Latihan 4.4 di halaman tersebut termasuk dalam bab 4 yang membahas tentang Kesebangunan Dua Segitiga.
Sebelum melihat kunci jawaban, diharapkan siswa dapat mengerjakan soal secara mandiri. Kunci jawaban ini ditujukan untuk orang tua sebagai panduan dalam mendampingi proses belajar anak. Perlu diingat, mungkin ada perbedaan antara jawaban pada kunci jawaban Matematika Kelas 9 SMP halaman 254 dan 255.
Latihan 4.4
Kesebangunan Dua Segitiga
Selesaikan soal-soal berikut ini dengan benar dan sistematis.
1. Pada gambar di samping, QR//ST. Q
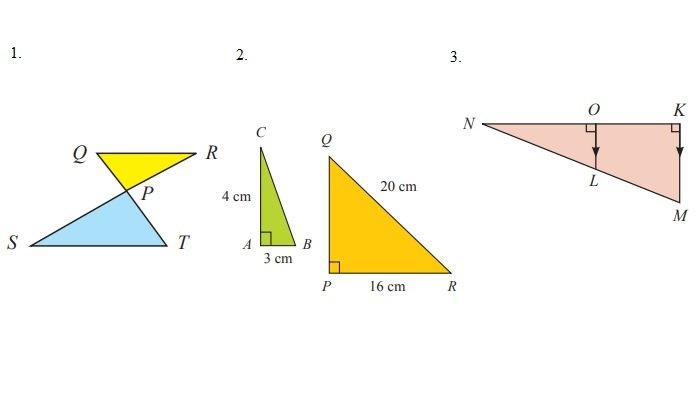
a. Buktikan bahwa ∆QRP dan ∆TSP sebangun.
b. Tuliskan perbandingan sisi-sisi yang bersesuaian.
Jawaban:
a) m∠RQP = m∠STP (berseberangan dalam)
m∠QRP = m∠TSP (berseberangan dalam)
m∠QPR = m∠TPS (bertolak belakang)
Jadi, ΔQRP dan ΔTPS sebangun karena memiliki sudut-sudut yang bersesuaian sama besar.
b) QR/TS = RP/SP = QP/TP
Baca juga: Perbandingan Volume: Kunci Jawaban Matematika Kelas 9 SMP Halaman 238 239 240 241 Kurikulum 2013
2. Perhatikan gambar berikut.
a. Buktikan bahwa ∆ABC dan ∆PQR sebangun.
b. Tuliskan perbandingan sisi-sisi yang bersesuaian.
Jawaban:
a) PQ = √20⊃2; - 16⊃2;
= √400 - 256
= √144
= 12
AB / PQ = 4/16 = 1/4
m∠BAC = m∠QPR = 90° (diketahui)
Jadi, ΔABC dan ΔPQR sebangun karena memenuhi syarat kesebangunan.
b) AB/PQ = AC/PR = BC/QR
3. Perhatikan gambar berikut.
Apakah ∆KMN sebangun dengan ∆OLN?
Tunjukkan.
Jawaban:
Iya,
m∠L (siku-siku)
m∠ (berhimpit)
m∠OLN = m∠KMN (sehadap karena OL //KM)
Jadi, ΔKMN dan ΔOLN sebangun karena sudut-sudut yang bersesuaian sama besar.
4. Pada ∆ABC dan ∆PQR diketahui m∠A = 105o, m∠B = 45o, m∠P = 45o, dan m∠Q = 105o.
a. Apakah kedua segitiga tersebut sebangun? Jelaskan.
b. Tulislah pasangan sisi yang mempunyai perbandingan yang sama
Jawaban:
a) Iya, karena dua pasang sudut yang bersesuaian sama besar, yaitu m∠A = m∠Q = 105° dan m∠B = m∠P = 45°.
b) AB dengan QP, BC dengan PR, dan AC dengan QR.
Baca juga: Kunci Jawaban Matematika Kelas 9 SMP Halaman 238 239 240 241: Lebar dan Tinggi Miniatur Batako
5. Perhatikan gambar.
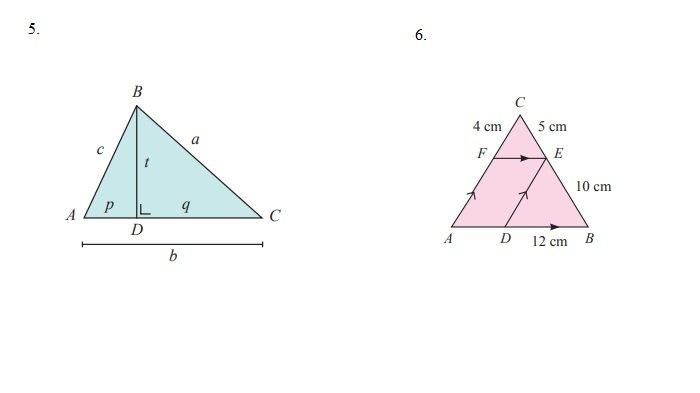
Diketahui m∠ABC = 90o, siku-siku di B.
a. Tunjukkan bahwa ∆ADB dan ∆ABC sebangun.
b. Tunjukkan bahwa ∆BDCdan ∆ABC sebangun.
Jawaban:
a) m∠BAD = m∠CAB (berhimpit)
m∠BDA = m∠CBA = 90° (diketahui siku-siku)
Jadi, ΔADB dan ΔABC sebangun karena memiliki dua pasang sudut yang bersesuaian sama besar.
b) m∠BCD = m∠ACB (berhimpit)
m∠CDB = m∠CBA = 90° (diketahui siku-siku)
Jadi, ΔBDC dan ΔABC sebangun karena memiliki dua pasang sudut yang bersesuaian sama besar.
6. Perhatikan gambar.
a. Tunjukkan bahwa ∆FCE ∼ ∆ACB.
b. Tunjukkan bahwa ∆FCE ∼ ∆DEB.
c. Tunjukkan bahwa ∆ACB ∼ ∆DEB.
d. Tentukan panjang FE dan AF
Baca juga: Kunci Jawaban Matematika Kelas 9 SMP Halaman 226: Tunjukkan Bahwa WXYZ Adalah Jajargenjang!
Jawaban:
a) ∠ CFE = ∠ CAB (sudut sehadap)
∠ CEF = ∠ CBA (sudut sehadap)
∠ FCE = ∠ ACB (sudut berimpit)
Jadi, ΔFCE sebangun dengan ΔACB.
b) ∠ CFE = ∠ EDB (sudut sehadap)
∠ CEF = ∠ DBE (sudut sehadap)
∠ FCE = ∠ DEB (sudut sehadap)
Jadi, ΔFCE sebangun dengan ΔDEB.
c) ∠ CAB = ∠ BDE (sudut sehadap)
∠ ABC = ∠ DBE (sudut berimpit)
∠ ACB = ∠ DEB (sudut sehadap)
Jadi, ΔACB sebangun dengan ΔDEB.
d) FE = CE x DB / BE
= 5 x 12 / 10
= 6
AF = BE x CF / CE
= 10 x 4 / 5
= 8
Jadi, panjang FE adalah 6 cm dan panjang AF adalah 8 cm.
Disclaimer:
- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.
- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.
| JAWABAN: Ekonomi Kelas 12 Halaman 30-38. Bab 1: Pertumbuhan & Pembangunan Ekonomi |

|
|---|
| Jawaban Bahasa Inggris Kelas 9 Halaman 64: What Family does Cendrawasih Belong to? |

|
|---|
| JAWABAN: Bahasa Indonesia Kelas 8 Halaman 30. Membubuhkan Tanda Baca Kalimat |

|
|---|
| Kunci Jawaban Bahasa Indonesia Kelas 5 Halaman 16: Antonim Hemat |

|
|---|
| JAWABAN: Pendidikan Pancasila Kelas 9 Halaman 26 Dan 27. Uji Kompetensi Bab 1 |

|
|---|






